【數(shù)學(xué)之美】分形——發(fā)現(xiàn)隱藏的維度
2020-11-07 09:12:17
次
仔細(xì)回想一下，在我們的生活中，無論是蜿蜒曲折的海岸線、綿延的山脊、變幻無常的云團(tuán)，盤根錯(cuò)節(jié)的樹根，還是人體的毛細(xì)血管，盡管它們的形狀是不規(guī)則的，但如果用不同倍數(shù)的鏡頭來觀察，它們的局部、分支和整體都有著非常高的相似性。
數(shù)學(xué)家們將這種“可以分成數(shù)個(gè)部分，且每一部分都（至少近似地）是整體縮小后的形狀“的形態(tài)特征叫做分形，最早由數(shù)學(xué)家曼德爾布羅特(B.B.Mandelbrot)在1973年提出。
盡管上述自然現(xiàn)象中的分形可能不那么完美，但是一旦我們利用數(shù)學(xué)公式，就可以構(gòu)造出各種各樣的完美分形。
數(shù)學(xué)里的分形
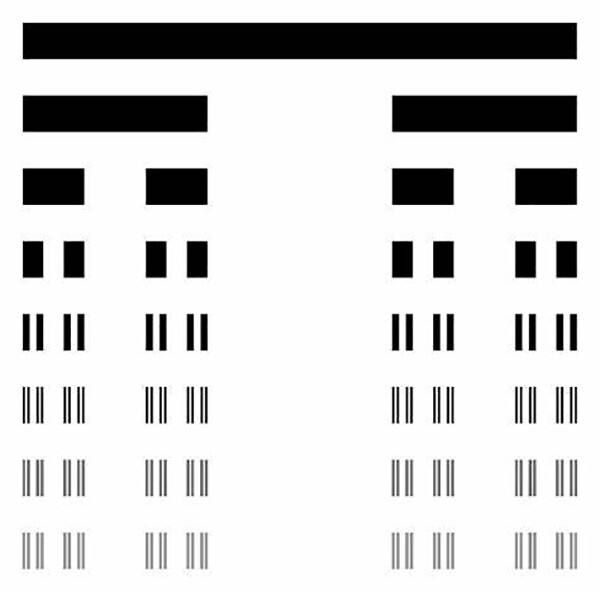
數(shù)學(xué)里的分形可以說是從康托爾集（Cantor Set）開始的。一個(gè)線段把中間的1/3去掉，得到兩個(gè)分開的線段，再對(duì)剩下的兩段進(jìn)行相同的操作，得到4個(gè)線段。這樣重復(fù)進(jìn)行下去直到無窮，最后得到的圖形集合就是康托爾集。用一個(gè)看似簡(jiǎn)單的步驟得到了一個(gè)無限復(fù)雜的圖形，而且它的每一個(gè)細(xì)節(jié)放大之后都和整體看起來一模一樣。
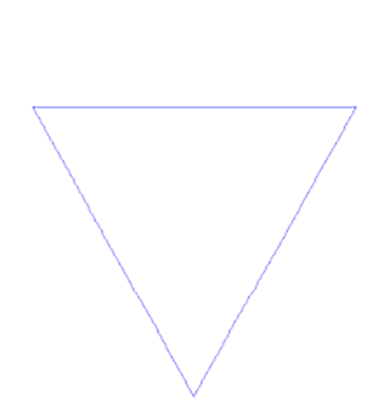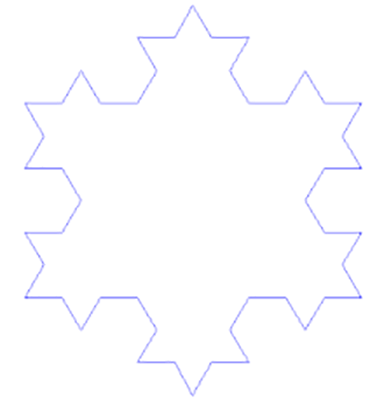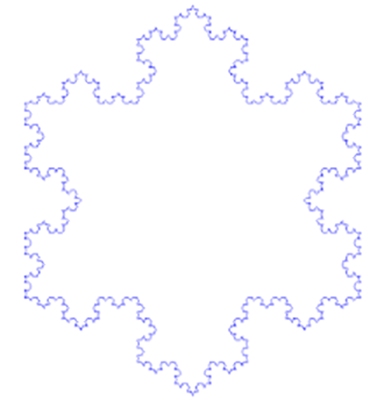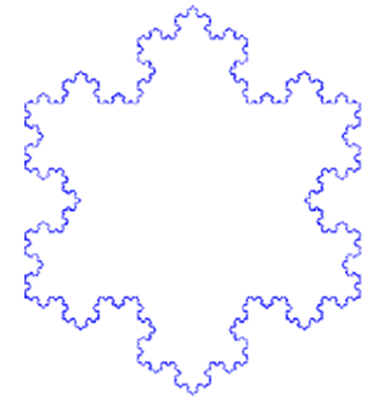
科克曲線（Koch snowflake）從一個(gè)正三角形開始，在它的每個(gè)邊上增加一個(gè)1/3大小的小三角，它就變成了一個(gè)六角星，接著在每個(gè)小三角的邊上繼續(xù)增加它的1/3大小的小三角，然后無限重復(fù)這個(gè)過程。就會(huì)得到一個(gè)看上去像是雪花的圖形。
如果說康托爾集是最平淡的分形，那么科克曲線才真正展示了分形之美。當(dāng)你放大之后，就會(huì)發(fā)現(xiàn)它的每一個(gè)邊都是自身形狀的無數(shù)次重復(fù)。不僅如此，這個(gè)圖形還有一個(gè)神奇的特性：它有著無限長(zhǎng)的邊長(zhǎng)，但是它的總面積卻最大不會(huì)超過雪花的外接圓面積。換句話說，一根無限長(zhǎng)的曲線圍住了一塊有限的面積。
一個(gè)更有代表性的分形圖案：皮亞諾曲線（Peano Curve）。一根線不斷構(gòu)造自相似的形狀，最終把正方形填滿。這樣一條本該是一維的曲線卻憑借分形特征填滿了二維的形狀，似乎已經(jīng)超越了一維的境界，但說它是二維圖形又還不夠。那它到底是一維還是二維呢？
曼德勃羅特集（mandelbrot set）以分形之父曼德爾布羅特的名字命名，可能是人類有史以來做出的最奇異，最瑰麗的幾何圖形，曾被稱為“上帝的指紋”。它集非常簡(jiǎn)單的產(chǎn)生公式和無限復(fù)雜的圖像為一體。有的地方像日冕，有的地方像燃燒的火焰，只要計(jì)算的點(diǎn)足夠多，不管你把圖案放大多少倍，都能顯示出更加復(fù)雜的局部。這些局部既與整體不同，又有某種相似的地方，好像有無窮無盡的細(xì)節(jié)和自相似性。
類似有趣的分形還有很多，我們一起來看些例子吧。
分形的應(yīng)用
我們身邊充斥著無處不在的分形，同時(shí)，我們也將分形的概念和方法應(yīng)用在諸多領(lǐng)域。
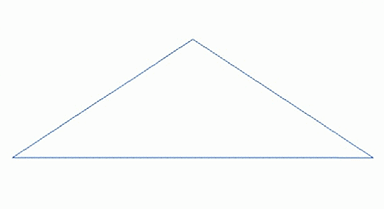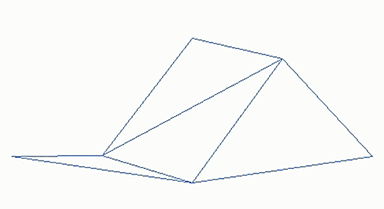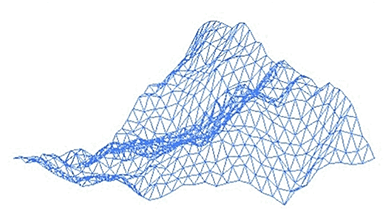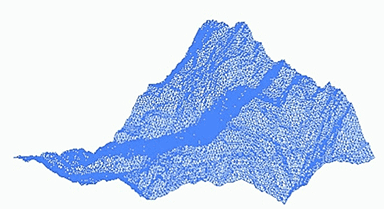
美國(guó)皮克斯公司的創(chuàng)始人之一、計(jì)算機(jī)科學(xué)家洛倫·卡彭特，用分形理論第一次在電腦繪制出讓人瞠目的3D山巒巨石。從一個(gè)全景圖出發(fā)，由一些非常粗略的三角形構(gòu)成，然后對(duì)于每個(gè)三角形，分成4個(gè)小三角形，繼續(xù)這樣迭代，最終形成了非常逼真的山脈。這一方法成為了現(xiàn)在電影、游戲中實(shí)現(xiàn)特效的重要方式。
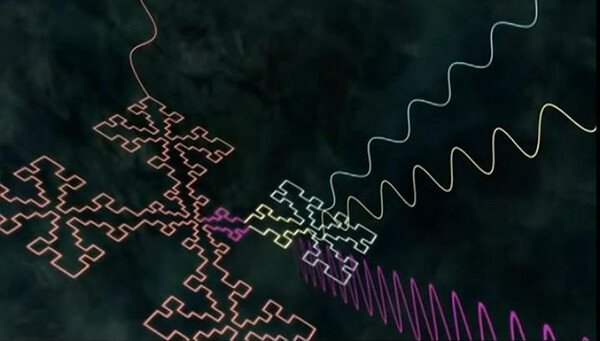
在無線電領(lǐng)域，如果你觀察用于信號(hào)接收的天線，你會(huì)看到優(yōu)美的自相似分形。通過分形設(shè)計(jì)讓線路在狹小的空間內(nèi)無限擴(kuò)展（工藝允許的情況下）長(zhǎng)度，不僅大大縮小天線的體積，還可以保證更好的收發(fā)效果。也正是因?yàn)榉中蔚膽?yīng)用，我們的手機(jī)才得擺脫了那些明顯的天線，做成現(xiàn)在這種精致的樣式。
美國(guó)PBS電視臺(tái)于2008年制作了一部名為《尋找隱藏的維度》的數(shù)學(xué)紀(jì)錄片，上述關(guān)于分形的所有內(nèi)容都將在這部紀(jì)錄片里得到更加生動(dòng)地介紹。如果你對(duì)分形已經(jīng)有了好奇，就趕緊點(diǎn)擊觀看吧！
觀看鏈接：https://www.bilibili.com/video/av15972423
Tempo商業(yè)智能平臺(tái)
Tempo人工智能平臺(tái)
Tempo數(shù)據(jù)工廠平臺(tái)
Tempo指標(biāo)平臺(tái)
Tempo數(shù)據(jù)治理平臺(tái)
Tempo主數(shù)據(jù)管理平臺(tái)
首頁(yè)
美林?jǐn)?shù)據(jù)
大數(shù)據(jù)分析與應(yīng)用
陜公網(wǎng)安備 61019002000171號(hào)
